L’Usage de la Régression de Processus Gaussiens en Fusion
L’énergie de fusion représente l’une des solutions les plus prometteuses pour répondre à la demande croissante d’énergie propre, renouvelable et durable. Elle repose sur le principe de fusionner deux atomes pour en créer un nouveau, libérant ainsi une énergie considérable. Bien que ce processus ait déjà été maîtrisé au sein du soleil, les chercheurs du monde entier s’efforcent d’en faire une réalité économique ici sur Terre.
L’IA au Service de l’Énergie de Fusion
L’intelligence artificielle (IA) et le machine learning (ML) jouent un rôle crucial dans l’accélération de la recherche sur l’énergie de fusion. Les techniques d’IA peuvent aider les scientifiques et ingénieurs à identifier des motifs cachés dans les diagnostics expérimentaux, fournissant ainsi des insights précieux sur la physique fondamentale des plasmas. Ces technologies permettent également d’optimiser les réglages des expérimentations, améliorant ainsi les performances et l’efficacité des dispositifs de fusion.
Lisez notre article : L’IA, un Pillier pour l’Avenir de la Fusion Nucléaire
La Régression de Processus Gaussiens (GPR) : Un Outil Clé
Récemment, Sapientai a publié un article de recherche intitulé “A Gaussian Process Guide for Signal Regression in Magnetic Fusion“, qui explore l’utilisation de la Régression de Processus Gaussiens (GPR) dans l’analyse des données issues des expériences de fusion magnétique. La GPR est un modèle d’apprentissage machine qui utilise les données connues pour prédire les valeurs inconnues, tout en fournissant une estimation de l’incertitude associée à chaque prédiction.
Lisez leur article de blog: How Best to Use a Gaussian Process Regression in Fusion
Comprendre la Régression de Processus Gaussiens (GPR)
La GPR repose sur plusieurs concepts clés :
- Corrélation spatiale : Le GPR suppose que les données proches les unes des autres ont des valeurs similaires, et qu’il est possible de suivre toutes les incertitudes des mesures.
- Mécanisme de prédiction : Pour estimer une valeur inconnue, le GPR considère les valeurs connues à proximité.
- Quantification de l’incertitude : Chaque prédiction est accompagnée d’une estimation de l’incertitude, fournissant ainsi une marge de confiance autour de la valeur prédite.
- Distribution gaussienne : L’incertitude est modélisée à l’aide d’une distribution gaussienne, en forme de cloche.
- Apprentissage adaptatif : Au fur et à mesure que de nouvelles données sont intégrées, le GPR ajuste ses prédictions et ses estimations d’incertitude.
L’Application de la GPR dans la Fusion
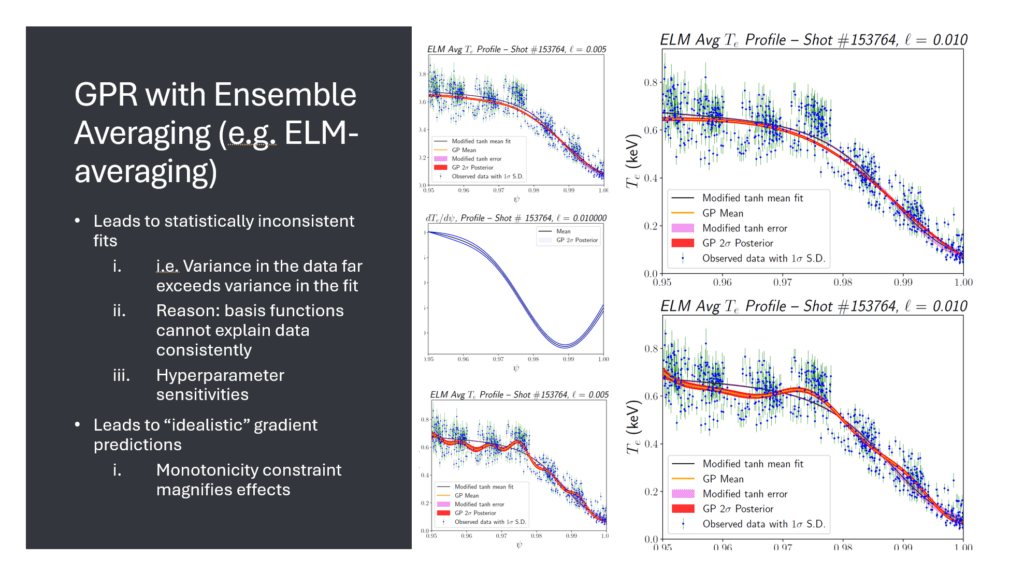
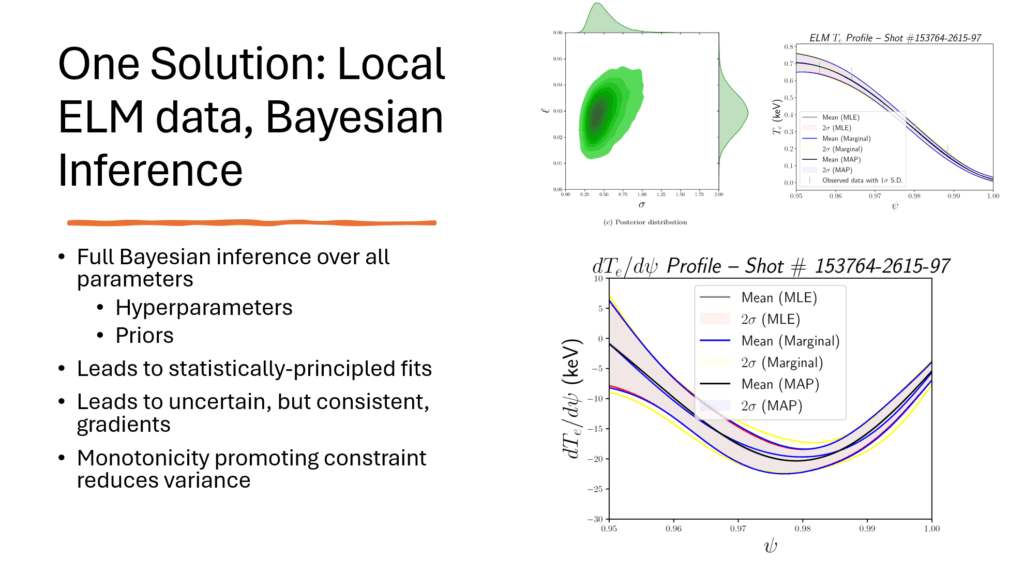
Dans le contexte des tokamaks, des dispositifs en forme de tore utilisés pour générer de l’énergie de fusion, le GPR peut jouer un rôle crucial. Les profils de température des électrons, par exemple, sont essentiels pour comprendre le comportement du plasma et améliorer les performances des dispositifs de fusion. En utilisant la GPR, les scientifiques peuvent obtenir des informations plus nuancées et plus fiables sur ces profils, ce qui peut guider les futures conceptions expérimentales.
Avantages et Précautions
Bien que la GPR offre une approche flexible et adaptable, elle nécessite une compréhension approfondie et une attention particulière pour éviter les mauvaises interprétations. L’article de Sapientai met en garde contre les choix de paramètres hyperparamétriques et souligne l’importance d’éviter les conclusions hâtives basées sur des données insuffisantes.
Conclusion : Vers un Futur Énergétique Durable
L’article de Sapientai montre que la GPR peut non seulement aider à extraire des informations précieuses des données de diagnostic de fusion, mais aussi à mettre en évidence les domaines où une collecte de données supplémentaire serait la plus bénéfique. En optimisant les techniques de fusion, la GPR pourrait bien jouer un rôle clé dans la réalisation du rêve d’une énergie de fusion abondante et durable.
Pour en savoir plus sur l’utilisation de la Régression de Processus Gaussiens dans la fusion magnétique, vous pouvez consulter l’article complet publié par Sapientai.